몇가지 정리
[정리1] 어떤 점 a와 그 점 a는 이어졌다.
[증명] 점 a와 점 a는 같은 선 위에 있고 그 사이에 다른점이 없으므로 이어졌다.(끝)
편의상 점위에 놓인 흑돌을 말할 때는 흑돌이란 용어를 그 흑돌이 놓여진 흑점과 구분하지 않고 쓰기로 한다. 백돌의 경우에도 마찬가지이다.
[정리2] 흑돌 a와 흑돌 b가 이어졌으면 흑돌 b와 흑돌 a도 이어졌다.
[증명] 흑돌 a와 흑돌 b가 이어졌으므로 정의에 의하여 다음과 같은 몇 개(n개라 하자)의 이어진 흑점들 1, 2, 3, … , n을 찾을 수 있다. 단, a와 1은 같은 선 위에 있고 그 사이에 다른 점이 없다. 1과 2는 같은 선 위에 있고 그 사이에 다른 점이 없다. 2와 3은 같은 선 위에 있고 그 사이에 다른 점이 없다. …. n과 b는 같은 선 위에 있고 그 사이에 다른 점이 없다. 이 때 같은 선 위에 있고 그 사이에 다른 점이 없는 두 점은 순서를 바꿔도 역시 같은 선 위에 있고 그 사이에 다른 점이 없으므로 여전히 이어졌다. 따라서 b에서 시작해서 이어진 흑점들 n, … , 3, 2, 1을 통과해서 a까지 올 수 있으므로 흑돌 b와 흑돌 a는 이어졌다.(끝)
[정리3] 흑돌 a와 흑돌 b가 이어지고 흑돌 b와 흑돌 c가 이어졌으면 흑돌 a와 흑돌 c도 이어졌다.
[증명] 흑돌 a와 흑돌 b가 이어졌기 때문에 흑돌 a에서 시작해서 이어진 흑돌만 통과해서 흑돌 b까지 올 수 있다. 그 다음 흑돌 b와 흑돌 c가 이어졌기 때문에 흑돌 b에서 시작해서 이어진 흑돌만 통과해서 흑돌 c까지 올 수 있다. 결국 흑돌 a에서 시작해서 이어진 흑돌만 통과해서 흑돌 c까지 올 수 있으므로 흑돌 a와 흑돌 c는 이어졌다.(끝)
[정리4] 어떤 흑돌이 죽은돌일 때 그 흑돌과 이어진 다른 흑돌도 모두 죽은돌이다. 어떤 흑돌이 산돌일 때 그 흑돌과 이어진 다른 흑돌도 모두 산돌이다. 어떤 흑돌이 죽은돌도, 산돌도 아닐 때 그 흑돌과 이어진 다른 흑돌도 모두 죽은돌도 산돌도 아니다. 백돌의 경우에도 마찬가지이다.
[증명]4-1. 어떤 흑돌 a가 죽은돌일 때 그 흑돌과 이어진 다른 흑돌 b가 있다고 하자. 흑이 먼저 기회를 가져도 백은 흑돌 a를 따낼 수 있기 때문에 백은 흑돌 a를 막힌돌로 만든다. 앞의 [정리3]에 의하여 흑돌 b와 이어진 흑돌은 흑돌 a와 이어졌고 막힌돌의 정의에 의하여 흑돌 a와 이어진 모든 흑돌은 빈점과 이어지지 않았기 때문에 흑돌 b와 이어진 모든 흑돌은 빈점과 이어지지 않았다. 따라서 흑돌 b는 막힌돌이 되었다. 백이 흑돌 b를 막힌돌로 만들었기 때문에 흑돌 b를 따낼 수 있다.(끝)
4-2. 어떤 흑돌 a가 산돌일 때 그 흑돌과 이어진 다른 흑돌 b가 있다고 하자. 백이 먼저 기회를 가져도 흑돌 a를 따낼 수 없기 때문에 백이 착수한 직후 흑돌 a는 막힌돌이 아니다. 이 때 흑돌 a와 이어진 흑돌중에 빈점과 이어진 어떤 흑돌 c가 반드시 있다. [정리2]에 의하여 흑돌 b와 흑돌 a가 이어졌고 [정리3]에 의하여 흑돌 b와 흑돌 c가 이어졌으며 흑돌 c는 빈점과 이어졌다. 따라서 흑돌 b는 막힌돌이 아니고 백은 흑돌 b를 따낼 수 없다.(끝)
4-3. 어떤 흑돌 a가 죽은돌도, 산돌도 아닐 때 그 흑돌과 이어진 다른 흑돌 b가 있다고 하자. 흑돌 b가 죽은돌이라 가정하면 [정리2]와 앞의 증명 4-1에 의하여 흑돌 a가 죽은돌이다. 이는 처음의 조건과 모순이다. 따라서 흑돌 b는 죽은돌이 아니다. 흑돌 b가 산돌이라 가정하면 [정리2]와 앞의 증명 4-2에 의하여 흑돌 a가 산돌이다. 이도 처음의 조건과 모순이다. 따라서 흑돌 b는 산돌도 아니다.(끝)
[참고] 이 [정리4]에 의하면 검증할 때 말썽돌 한 개 한 개 마다 모두 할 필요는 없고
이어진 한 덩어리 한 덩어리 마다 해도 됨을 알 수 있다.
[정리5](마지막 정리) 한 판의 바둑의 종류는 무한히 많다.
용어의 정의.
기보: 바둑판에 있는 361개의 모든 점에 이름을 붙이고 여기에 착수포기라는 이 름 한 개를 더한 후 어떤 한 판의 바둑에 대하여 처음부터 계가(또는 불계)에 이 르기까지의 모든 기회 사용의 내용을 이 362개의 이름으로 순서대로 적은 것.
서로 같은 한 판의 바둑: 한 판의 바둑 A와 한판의 바둑 B에 대하여 A의 기보와 B의 기보가 서로 같을 때 “A와 B는 서로 같다”고 말하고 A의 기보와 B의 기보가 서로 다를 때 “A와 B는 서로 다르다”고 말한다.
장면: 바둑판위의 361개의 점이 흑점인지 백점인지 빈점인지 모두 결정된 상태. [참고] 막힌돌을 그대로 올려놓고 있을 때의 장면과 들어낸 후의 장면은 서로 다르다. 361개의 점이 모두 빈점인 텅 빈 바둑판도 한 개의 장면이다(장면0 라 고 쓴다). 모두 흑돌로 채워진 모양, 모두 백돌로 채워진 모양도 각각 한 개의 장면이다. 장면의 개수는 모두 3×3×3×…×3(361개의 곱)개 있다.
연결장면: 바둑의 규칙에 따라 한 번씩 기회를 행사하였을 때마다 나타나는 장면들 을 나타나는 순서대로 연결해 놓은 것. 어떤 장면a에서 한번 기회를 행사하여 장 면b가 되었을 때 연결장면ab라 쓴다. [참고] 장면은 가장 짧은 연결장면이다. 연결장면abccddd에서 보면 장면c에서 한 번 착수포기가 있었고 장면d에서 두 번의 착수포기가 있어서 계가에 이르렀음을 알 수 있다.
순환장면: 특정한 연결장면이 연속해서 두 번 이상 이어진 연결장면.
[참고] 순환장면abababab는 있을 수 없다. 두 번째 장면이 패의 금지규정 때문에 나타날 수 없다. 순환장면abcdefabcdef를 가리켜서 삼패라 부른다.
줄여쓰기: 순환장면abcabc를 간단히 줄여서 (abc×2)라 쓰기로 한다.
순환장면bbcdbbcdbbcd는 (bbcd×3)으로
순환장면abbabbabbabbabbabb는 (abb×6)으로 등이다.
[증명]5-1.(순환장면을 허용하는 약한 조건일 때의 증명)
우선 다음과 같이 장면0,a,b,c,d,e,f를 정한다.

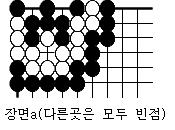
• • •
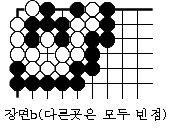
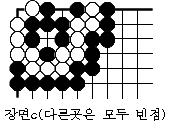
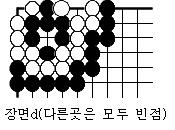


• • •
이제 여러 종류의 한 판의 바둑을 연결장면으로 나타내보면 다음과 같다.
1종류: 연결장면0…abcdef…
2종류: 연결장면0…(abcdef×2)…
3종류: 연결장면0…(abcdef×3)…
4종류: 연결장면0…(abcdef×4)…
•
•
•
•
n종류: 연결장면0…(abcdef×n)…
•
•
여기에서 연결장면0… 이란 장면0 다음부터 장면a직전까지의 연결장면을 생략했음을 뜻한다. 줄 끝에 나오는 … 표시는 장면f 다음부터 계가(또는 불계)에 이르기까지의 연결장면을 생략했음을 뜻한다. … 표시한 부분에는 순환장면abcdef가 없는 것으로 한다. 이제 위에 열거한 한 판의 바둑은 모두 서로 다름이 명백하다. 어떠한 큰 수 n 이 있어도 n종류보다 많은, 서로 다른 한 판의 바둑을 만들 수 있으니 한 판의 바둑의 종류는 무한히 많다.(끝)
5-2.(순환장면을 불허하는 강한 조건일 때의 증명)
순환장면이 없는 한 판의 바둑도 그 종류가 무한히 많음을 증명하겠다.
숫자판 10개의 정의.
다음과 같은 10개의 장면을 숫자판1,숫자판2,…,숫자판9,숫자판0이라 부르기로 한다.
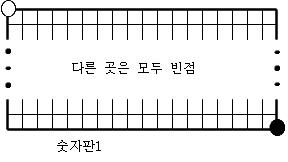
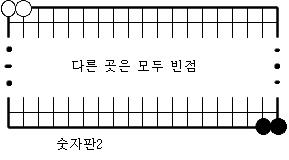
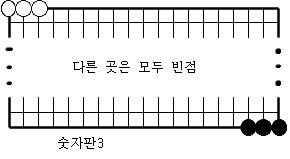
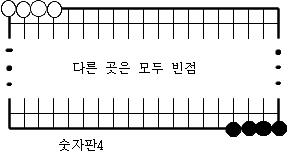
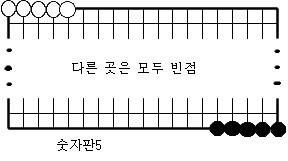
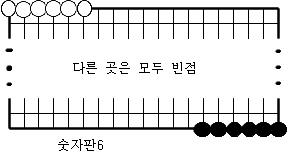


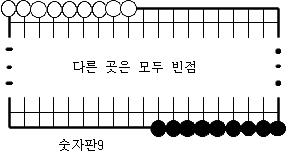
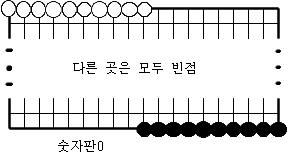
[보조정리1] 어떤 숫자판a에서 시작하여 어떤 숫자판b까지의 연결장면중에 순환장면도 없고 원치않는 다른 숫자판도 생기지 않도록 할 수 있다.
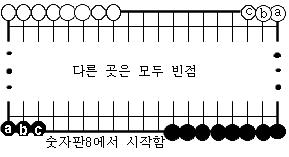
와 같이 흑a,백a,흑b,백b,흑c,백c,…와 같은 방법이다. 한줄이 다 메워지면 바로 곁에 있는 새로운 줄을 메워나간다. 새로운 줄부터는 항상 진행방향이 처음 숫자판에서 한 줄 메우던 방향과 반대이다. 이윽고 가운데에서 한 개의 빈점만을 
그 다음 흑이 백돌 360개를 따내면
오른쪽 그림과같은 장면이 된다. 이어서 백a, 흑b, 백c, 흑d, 백e에 놓으면 숫자판3이 만들어진다. 숫자판3이 아닌 다른 숫자판이라도 만들 수 있음은 명백하다.
처음에 숫자판8에서 시작하지 않고 다른 숫자판에서 시작하더라도 따내는 돌의 개수와 순서는 언제나 같다. 위에서 적은 180, 90, 45, 338, 169, 276, 138, 69, 326, 163, 279, 221,……, 4, 2, 1개 그리고 360개 그대로이다.(만약 시작할 때 백이 먼저 놓으면 따내는 돌의 숫자는 그대로이고 돌의 색만 반대가 되어 나중에는 흑돌대신 백돌이 한 개 남게되는데 숫자판 만드는 데는 아무 지장이 없다.)
위에 적은 숫자들을 보면 모두 다르다. 따라서 두 숫자판 사이의 연결장면중에 순환장면은 없다. 또 숫자판에서 처음 시작할 때와 나중에 숫자판을 만들 때의 착수순서를 보면 두 숫자판이 아닌 다른 숫자판은 만들어지지 않는다.(끝)
[보조정리2] 각 항이 숫자 0,1,2,3,…,9 로 이루어지고 다음 조건을 만족하는 무한수열이 존재한다. 조건: 임의의 항부터 시작해서 연속된 짝수개의 항을 택했을 때 앞의 반의 배열과 뒤의 반의 배열이 항상 서로 다르다.
[증명] 이 보조정리의 증명은 생략한다. 바둑의 본질과 너무 동떨어졌기 때문이다. 사실은 숫자 1,2,3만으로도 그러한 수열을 만들 수 있는데 어떤 200개만 나열해보면 다음과 같다.
1,2,1,3,1,2,3,1,3,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,2,1,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,2,1,3,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,2,1,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,1,3,2,1,2,3,1,2,1,3,1,2,3,2,1,2,3,1,2,1,3,2,1,2,3,2,1,3,1,2,3,2,1,2,3,1,2,1,3,2,1,2,3,2,1,3,2,3,1,2,1,……이 수열에서 예를 들어 7번째 항부터 6개의 항을 택해보면 3,1,3,2,3,1인데 앞의 3개항 3,1,3과 뒤의 3개항 2,3,1은 서로 다른 배열이다.(끝)
증명5-2의 완결. 위 [보조정리2]의 조건을 만족하는 어떤 무한수열을 한 개 택했다고 하고 이 수열을 처음의 수열이라 부르자. 이 수열의 n번째항의 숫자를 k라 할 때 k는 0,1,2,3,…,9중의 한 숫자일 것이다. 이 때 숫자판k를 장면n이라 정의하자. 장면1, 장면2, 장면3, … 에 나오는 흑돌의 개수를 차례로 적으면 처음의 수열과 같아질 것이다(단 흑돌이 10개 있을 때는 0으로 적는다).
이제 여러 종류의 한 판의 바둑을 연결장면으로 나타내보면 다음과 같다.
1종류: 연결장면0*1*
2종류: 연결장면0*1*2*
3종류: 연결장면0*1*2*3*
4종류: 연결장면0*1*2*3*4*
•
•
•
•
n종류: 연결장면0*1*2*3*…*n*
•
•
여기에서 연결장면0*1 이란 장면0부터 장면1까지의 연결장면을 뜻하며 그 사이의 장면중에는 숫자판과 순환장면이 없는 것으로 한다. 각 줄의 끝에 있는 * 는 계가(또는 불계)에 이르기까지의 연결장면을 뜻하며 그 중에는 숫자판과 순환장면이 없는 것으로 한다. 숫자와 숫자 사이의 * 는 [보조정리1]에서 설명한 연결장면을 뜻하며 당연히 그 중에는 숫자판과 순환장면이 없다. 마지막줄의 1*2*3*…*n 이란 1부터 n까지의 숫자 사이마다 *를 넣어서 써놓았음을 뜻한다. 위에 열거한 한 판의 바둑이 모두 서로 다름은 자명하다.
이제 연결장면0*1*2*3*…*n* 중에 순환장면이 있는가를 살펴보자.
먼저 이중에 순환장면이 있다고 가정하고 그 중에서 가장 짧은 순환장면에 포함되는 숫자판을 앞에서부터 차례로 장면(m+1), 장면(m+2),…, 장면(m+i), 장면(m+i+1), 장면(m+i+2), …, 장면(m+i+i) 라 하자. 가장 짧으므로 순환장면의 수는 짝수개이며 숫자판도 짝수개(2i개로 함)이다. 이 때 장면(m+1)은 장면(m+i+1)과 같고, 장면(m+2)는 장면(m+i+2)와 같고, … ,장면(m+i)는 장면(m+i+i)와 같다. 따라서 이들 2i개의 장면에 나오는 흑돌의 개수를 차례로 적으면(단,흑돌이 10개 있을 때는 0으로 적는다) 앞의 i개와 뒤의 i개가 같은 배열이 된다. 이는 처음의 수열이 갖는 조건에 모순이다. 따라서 순환장면이 있다는 가정은 거짓이다.
어떠한 큰 수 n 이 있어도 n종류보다 많은, 순환장면이 없는 서로 다른 한 판의 바둑을 만들 수 있으니 한 판의 바둑의 종류는 순환장면이 없는 것으로도 무한히 많다.(끝)
[정리6](마지막을 넘은 정리) 한판의 바둑의 종류보다 신의 바둑의 종류가 더 많다.
용어의 정의.
신의 바둑: 계가나 불계에 이르지 않고 한없이 착수가 이루어지는 바둑.
신의 바둑의 기보: 361개의 점에 착수포기까지 더한 362개의 이름을 사용하여 신 의 바둑을 기록한 무한수열.
서로 같은 신의 바둑: 신의 바둑 A와 신의 바둑 B에 대하여 A의 기보와 B의 기보 가 서로 같을 때 “A와 B는 서로 같다”고 말하고 A의 기보와 B의 기보가 서로 다를 때 “A와 B는 서로 다르다”고 말한다.
X종류보다 Y종류가 더 많다: X종류 한 개와 Y종류 한 개를 서로 짝짓고, 남은 X 종류중 한 개와 남은 Y종류중 한 개를 또 짝짓고 … 이와 같이 서로 짝지어서 X 종류 모두를 짝지어도 짝짓는 방법과 관계없이 반드시 Y종류가 남는다.
[증명] 한 판의 바둑의 종류와 신의 바둑의 종류를 서로 짝지어서 한 판의 바둑의 모든 종류가 짝을 찾았다고 가정하자. 이 때 신의 바둑의 종류가 남음을 증명하기로 한다. 어떤 한판의 바둑 남에 대하여 그의 짝인 신의 바둑이 여일 때 (남,여) 라 쓰고 이들을 한 쌍의 바둑이라 부르자. 지금부터 한 쌍의 바둑들을 한줄로 세우기로 한다. 먼저 단 한 번의 기회에서 이루어진 한 판의 바둑을 남1 이라 하고 그의 짝을 여1 이라 하자(남1은 흑이 바둑판앞에 앉자마자 불계선언한 한판의 바둑임). 그래서 (남1,여1) 한 쌍의 바둑이 맨 앞에 줄섰다. 그 다음 두 번째 기회에서 이루어진 한 판의 바둑들을 적당히 줄세워서 남2,남3,남4,…,남364라 하고 그들의 짝을 여2,여3,여4,…,여364라 하자. 그래서 한 쌍의 바둑들 (남2,여2), (남3,여3), (남4,여4), …, (남364,여364)이 줄을 선다. 그 다음 세 번째 기회에서 이루어진 한 판의 바둑들을 그의 짝들과 함께 줄세워서 (남365,여365), (남366,여366), … 이런 방법으로 모든 한 쌍의 바둑들을 줄세웠다고 하자. 한 판의 바둑은 어떤 종류든지 이 줄 어디엔가 서 있음은 자명하다. 그러나 신의 바둑은 그렇지 않은데 다음 한 종류의 신의 바둑
연결장면0…1*2*3*4*5*… 을 살펴보자.
여기에서 연결장면0… 이란 장면0 다음부터 장면1직전까지의 연결장면을 생략했음을 뜻하며 여기에는 숫자판이 없는 것으로 한다. 그 다음부터는 자연수1,2,3,4,…를 무한히 이어쓴 것이고 숫자와 숫자 사이의 * 는 [정리5][보조정리1]에서 설명한 연결장면을 뜻하며 당연히 그 중에는 숫자판이 없다.
여기에서 장면1,장면2,장면3,…는 모두 숫자판인데 다음과 같이 만들었다. n이 1,2,3,…일 때 장면n은 앞에서 줄세운 신의 바둑 여n중에서 n번째 나오는 숫자판과 다른 숫자판이다(만약 여n중에 n번째 숫자판이 없으면 임의의 숫자판으로 한다). 이렇게 만들어진 연결장면0…1*2*3*4*5*…는 여1, 여2, 여3, 여4, … 들의 어느 것과도 최소한 한 개의 숫자판은 다르기 때문에 그들 어느것도 아니다. 즉, 신의 바둑인 연결장면0…1*2*3*4*5*…는 짝이 없다. 따라서 한 판의 바둑의 종류보다 신의 바둑의 종류가 더 많다.(끝)
[참고] 같은 무한이라 해도 한판의 바둑의 종류보다 신의 바둑의 종류가 한 단계(연속체가설수용) 더 많음이 증명되었다. 한판의 바둑, 또는 신의 바둑의 종류와 인생의 종류를 비교하면 어떤 쪽이 더 많을까? 여기에서 인생이란 이미 이루어진 것 뿐만 아니라 장차 이루어질 수도 있는 가상의 인생까지 말한다. 기껏해야 한판의 바둑의 종류를 넘지 못한다고 말하는 사람도 있을 것이다. 왜냐하면 한 사람은 한 가지 인생을 살아가는데 앞으로 태어날 한 사람마다 한 판의 바둑과 짝지으면 한명도 남는 사람이 없도록 할 수 있으니까! 한편 신의 바둑의 종류를 넘는다고 믿는 사람도 있을 것이다. 왜냐하면 태어날 한 사람의 미래는 아직 결정된 것이 아니라 그 사람의 자유의지로 그 사람이 만들어가는 것이니까! 그 사람은 감동적인 노래를 작곡할 수도 있고 난해한 추상화를 그릴 수도 있다. 그런데 한 장의 그림의 종류만 해도 신의 바둑의 종류보다 한 단계(일반연속체가설수용) 더 많다! 신의 바둑의 종류보다 한 단계 더 많은 종류에서의 선택을 창조라 정의하자. 사람들은 자신들의 삶을 자신들 스스로 창조해 간다고 나는 믿는다. 그래서 신의 바둑의 종류보다 인생의 종류가 더 많다고 나는 믿는다.(모두 끝)
주)연속체가설(continuum Hypothesis): 모든 자연수의 개수보다는 많고 동시에 모든 실수의 개수보다는 적은 무한은 없다는 수학의 가설. 수용하거나 말거나 모순없음이 밝혀졌다.
'퍼온~바둑..! > 다른 구성들~' 카테고리의 다른 글
| [=] 바둑의 정의2(보충) (2) | 2008.06.02 |
|---|---|
| [=] 바둑의 정의1 (0) | 2008.06.01 |
| [=] 기타 (0) | 2008.05.24 |
| [=] 원시기법 (0) | 2008.05.24 |
| [=] 바둑의 규칙 (0) | 2008.05.24 |