서양인들에 의해 주도되어 온 바둑 연구의 분야들
1) 바둑에 관한 기존의 심리학적 연구들
2) 바둑에 관한 기존의 수학적 연구들
3) 컴퓨터바둑과 관련한 기존의 연구들
장영호는 매우 용감하게 속내를 드러낸다. 한 칼럼에서 그는 서양인들이 바둑을 학문의 중요한 테마로 연구한다는 데 대해 이렇게 두 가지 의문을 제시한다. 첫째, "바둑의 원리조차 잘 모르는 서양인들이 무슨 학문적 연구를 할 수 있겠는가?" 둘째, "설령 연구를 한다 하더라도 도대체 바둑의 무엇을 어떻게 수학적으로 규명하겠다는 것인가?"
바둑과 현대과학이 여러 공통점이 있다고 보면서 "바둑 원리 (규칙) 들을 수학적 논리를 사용하여 쉽게 설명할 수 있다" 는 점을 들고 있는 점 역시 날카롭다. 그는 과학이라는 영광된 칭호는 "지식의 어떤 분야가 자연 연구에 도움을 주는 결과를 가져오던가 인간이 일상 생활을 하는데 그것을 이용할 경우" 에 주어지는 것이라 가정하면서 "바둑을 둘 때 최적의 연속수를 두었다고 할지라도 바둑판 이외에는 어디서든지 그 수가 쓰이지 않는다" 는 것은 분명하기 때문에 "솔직히 말해서 바둑을 과학으로 취급할 수는 없다" 고 고백한다. 라자레프는 이 지점에서 미묘한 사고의 혼란을 보여 주고 있는데, 왜냐하면 똑같은 이야기를 수학 (Mathematics) 에 대해서도 할 가능성을 배제할 수 없고, 또 자연 연구에 수학이 응용되는 것 못지않게 삶을 살아가는 데서 다양한 방식으로 바둑이 응용되고 있기 때문이다. 그러나 이런 단서를 붙인다 해도 여전히 크게 보아 그와 필자의 입장은 일치하는 것으로 보인다. 그도 또한 "현대과학 역시 어떤 틀에 맞출 수 없는 (인간의 직관력 같은) 수많은 요소들을 취급하지 않으면 안된다" 는 점을 잘 알고 있고, 또 "바둑에 관한 문제들은 인간이 직면해야 하는 자연의 난문제에 비하면 대단히 간단하다" 고 볼 수 있으므로 바둑을 그 어려운 문제들을 다룰 "새로운 수학적 도구와 방법을 연구개발하기 위한 시험대" 로 볼 수 있다고 생각하기 때문이다. 그는 "이것이야말로 현대과학과 인류를 위한 바둑의 역사적 사명" 이라고 믿는 것으로 보이며, 필자는 이렇게 한 문단 안에서 심오한 주장을 명쾌하게 펼 수 있었던 것은 라자레프가 수학자이기 때문이라 여기면서 박수 갈채를 보내고 싶은 심정이 된다.
1) 바둑과 과학
2) 경영예술로서의 바둑
3) 바둑의 수학적 특성과 그 특성을 현대 과학과 경제학에 적용
(1) 컴퓨터 과학과 인공지능 (Artificial Intelligence)
(2) 컴퓨터 과학과 정보과학
(3) 최적화 (Optimization) 이론과 경제학 (Economics)
(4) 인공두뇌학 (Cybernetics)
1) 바둑에 관한 기존의 심리학적 연구들
버마이스터가 운영하는 홈페이지 'http://psy.uq.edu.au/~jay/' 의 Paper 에 올려져 있는 "An Introduction to the Computer Go Field and Associated Internet Resources" 의 제 4 절 「컴퓨터바둑 분야의 역사」에는 학술적 연구에 할애된 첫번째 소절에서 조브리스트 (Zobrist) 의 연구, 라이더 (Ryder) 의 연구, 그리고 리트먼 과 윌콕스 (Walter Reitman and Bruce Wilcox)의 연구 등이 소개되고 있다.
최일호 교수는 데 그루트 및 체이스와 사이먼에 의거하여 체스에 관한 심리학적 연구의 주요 과제로 "선택적 탐색, 패턴재인 (Pattern Recognition) 의 중요성, 점진적 수준 향상과 전문가의 탁월한 기억능력" 을 꼽았고, 고버트 (Gorbet, 2000) 에 의거하여 체스 전문가들의 기억수행 연구의 주요 방향을 1) 지각 (Perception) 과 패턴 재인의 주요성, 2) 단기기억 (Short Term Memory) 과 장기기억 (Long Term Memory)의 상대적 역할, 3) 이론적으로 가정되는 청크의 존재, 상위 수준 지식의 역할에 대한 연구에서 찾고 있다.
2) 바둑에 관한 기존의 수학적 연구들
3) 컴퓨터바둑과 관련한 기존의 연구들
바둑이 학문적으로 연구되지 못했다는 점이 결국 정답이리라 믿는다. 외국과 비교해 볼 때 바둑, 그리고 컴퓨터바둑에 관한 학문적 연구는 정말 거의 전무하다고 밖에 할 수 없다. 정수현 교수나 문용직 박사 역시 선행 연구의 희귀성에 절망하고 외로운 여행자의 심경을 토로하는 모습을 보이지 않았는가! 그러나 '거의 전무하다고 할 수밖에 없는 것' 과 '전무한 것' 사이에는 명백히 천양지차가 있다. 과연 우리에게는 컴퓨터바둑에 관한 선행 연구가 전무한가?
무엇보다도 김영상, 이종철은 그들이 개발한 프로그램 <큰돌 (Keundol)> 이야기가 소개되고 있어 반갑기 짝이 없다. <큰돌> 은 1991 년부터 인공지능 프로젝트로 시작되었다고 하며, 그들의 이론적 연구와 아울러 "객체 지향적 개념을 사용하여 바둑판의 반면에 존재하는 요소 사이의 유기적 관계로서 <큰돌> 의 단면을 기술" 한다고 한다. <큰돌> 이라는 이름이 무엇을 의미하는지는 어렵지 않게 짐작할 수 있다. '큰 돌' 을 영어로 음역하면 그렇게 될 가능성이 높으니까 말이다. 실제로 서양인들은 최근에는 'Keundol' 이 아니라 'Big Hand' 로 이종철 교수의 프로그램을 호칭하는 것으로 보인다. 직접 의미를 물어 보고 나서 개명을 권유했는지, 이 교수 스스로 고친 것인지는 알 길이 없지만, 아무튼 재미있다.
국제대회에 명함을 내밀었던 국내의 컴퓨터바둑프로그램은 그렇다면 최소한 <큰돌> <Go Master> <FunGo> <Sason> 등이 존재하는 셈이다. 그렇다면 그 후 이들의 용쟁호투는 어떻게 전개되어 갔고, 그 결과 오늘의 무림 맹주는 어느 프로그램인 것일까?
예컨대 뮐러의 박사학위 논문과 김영상의 박사학위 논문은 컴퓨터바둑에 많이 응용되는 이론으로 고전적 게임이론 (Game Theory), 게임한정 (game specific) 이론, 휴리스틱 (Heuristic), 그리고 조합게임이론 (Combinatorial Game Theory) 을 꼽고 있다.
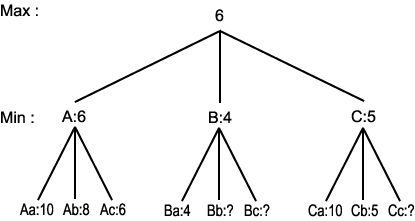
Martin Müller 와 김영상 이 고전적 게임이론 (Game Theory) 에서의 기법으로 의미하는 바는 무엇인가? 뮐러는 우선 고전적 게임 이론이 폰 노이만 (John von Neumann) 등의 개척자들에 의해 개발되었다는 점을 지적하고, 폰 노이만의 2 인 게임의 모델에서 경기자는 종국에 이르기까지 번갈아 가며 착수하며, 종국의 시점에서 승패는 평가함수 (Evaluation Function) 에 의해 결정된다는 점을 친절하게 상기시킨 다음, 최대최소 규칙이 게임이 종료되지 않은 상태에서 최선의 수를 찾아내는 데 이용될 수 있다고 쓰고 있다. 레이몬 (Ramon) 과 불로킬 (Blockeel) 은 최소-최대 검색 기법을 이렇게 설명한다. "두 명의 선수는 최대 Max 와 최소 Min 로 불린다. 최대는 게임의 결과를 최대화 시키려고 노력하고, 최소는 최소화 시키려고 노력한다. 최소최대 (Mini-max) 알고리즘에서 먼저 전체의 게임 트리 (Tree) 가 세워지고 그 다음에 거꾸로 평가를 하는 것이다. 각 기점에서, 만일 최대가 움직이면 하위기점의 최대값을 취하며, 만일 최소가 움직이려면 하위기점의 최소값을 취하는 것이다." 누구라도 금방 깨달을 수 있듯이, 바둑에서 우리는 완전한 게임 트리를 만들 수 없다. 그래서 최소-최대 검색 안에서 또 여러 가지 기법들이 고안되게 되고, 뮐러는 알파베타 가지치기 (Alpha-Beta Pruning), 전위표 (transposition table), 병행 검색 (Parallel search) 등을 예로 들었다. 이 중 가장 잘 알려진 알파-베타 가지치기를 레이몬과 블로킬은 다음과 같이 아주 알뜰하게 잘 설명하고 있다.
'알파-베타 가지치기' (alpha-beta pruning) 방법은 최소-최대 알고리즘을 단순히 최적화시키는 것이다. <표 6> 를 살펴보자. 기점 A 에서, 최소는 6 이라는 값을 가진 가지 Ac 를 선택할 것이다. 그 다음, 우리는 기점 B 를 살펴보자. 먼저 4 값을 가진 Ba 를 살펴보자. 우리는 이제 최대의 가지 B 는 결코 선택하지 않을 것이라고 추론할 수 있다. 왜냐하면 가지 B 의 값은 최대 4 를 넘지 않기 때문이다 (최소의 선택에 의해서). 이는 6 보다도 작은 값이다. 그러므로, 우리는 Bb 와 Bc 는 평가할 필요가 없는 것이다. 이와 유사하게, Ca 와 Cb 를 평가한 후, 5<6 이므로 우리는 Cc 를 평가할 필요가 없는 것이다.
<표 5> 알파-베타 가지치기
게임한정 이론을 설명하기 위해 Martin Müller 는 체스에서 한 쪽은 왕과 승정, 그리고 기사를 가지고 상대방은 왕만 가지고 승부를 겨루는 식의 하부 게임을 들면서 그런 특수한 게임의 문제를 해결하기 위해 개발된 특별한 이론들이 많다고 보고한다. 바둑에서의 그런 부분 게임에 관한 특별 이론으로 그는 렌츠 (Lenz) 의 수상전 공식과 벤슨 (Benson) 의 완생 탐지 알고리즘을 들었다.
휴리스틱스 (Heuristics) 란 엄격한 이론은 아니지만 바둑 격언들처럼 적시적소에서 잘 활용할 경우 크게 도움이 되는 요령 정도로 이해할 수 있을 것이다. 또 뮐러가 지적하듯 전형적인 맥, 사활과 수상전에서의 급소 모두가 휴리스틱한 수 생성 규칙으로 이해될 수 있다. 따라서 구태여 강조하지 않아도 실질적으로 모든 컴퓨터바둑 프로그램들이 휴리스틱스를 이용한다고 보아 마땅하다.
조합게임이론 (Combinatorial Game Theory) 에 관해서는 앞에서 이미 논의하였으므로, 이제 우리는 컴퓨터바둑 프로그래머들이 그 동안 대충 어떤 이론들을 무기 삼아 프로그램 개발 연구를 수행해 왔는지를 짐작할 수 있다. 뮐러와 김영상이 어떤 기준이나 척도에 의해 이 이론들을 네 가지 유형으로 분류했는지는 생각 외로 분명하지 않다. 필자의 느낌으로는 컴퓨터바둑 프로그램 개발의 역사, 좀더 구체적으로는 컴퓨터 체스 프로그램 개발에서 효과적이었던 기법과 이론들을 무작정 컴퓨터바둑프로그램 개발에 적용하는 과정에서 직면하게 된 의외의 문제들에 임시변통 격으로 대응해 온 역사가 오히려 이 이론들의 성격과 기능, 그리고 역할을 이해하는 데 도움이 된다. 좀 더 부연한다면, 컴퓨터 체스에서와 달리 고전적 게임이론에 바탕을 둔 검색 (Search) 트리의 방법이 체스 (Chess) 와는 비교할 수 없을 정도의 복잡성을 지닌 바둑의 난해함 때문에 뮐러와 김영상이 열거한 여타 이론들의 정립과 발전을 요구했다고 크 그림을 그려 볼 수 있겠다. 경우의 수가 너무 많아서 검색 트리 방법에는 한계가 있다. 그 방법 내에서 '알파-베타 가지치기' 기법처럼 더욱 정교한 방법들을 동원한다 해도 사정은 별로 나아지지 않는다. 그렇다면 아홉줄 바둑처럼 열아홉줄 바둑의 부분이라 할 수 있는 게임 (Game) 에 특수한 이론을 개발하여 그것을 전체에 일반화하는 방법을 써 보자. 또 한 판의 바둑을 바둑두는 이들이 포석, 중반, 끝내기로 나누는데, 그렇게 단계별로 나누어 적용하는 이론을 달리하여 보자. 정석 사전 데이터베이스를 입력하거나, 사활 묘수풀이 사전 데이터베이스를 입력하는 등 바둑에 관한 지식을 컴퓨터에게 많이 제공해 보자. 그래도 안 되면, 그 지식을 상황에 따라 응용할 수 있도록 휴리스틱한 지침들을 입력하도록 하자. 조합게임 이론에 의해 끝내기 영역에서 상당한 성과가 얻어졌으니 만큼 바둑 전체를 부분의 단순한 합으로 가정하고 그 결과를 바둑 전체에 응용해 보도록 하자. 뭐 이런 식으로 접근해 온 것이 아닐까?
문외한이 뭐 이렇게 알지도 못하는 이야기를 떠벌리느냐고 노발대발하는 독자들이 제법 될 것 같아 한시 바삐 줄행랑치고 싶은 마음뿐이다. 그러나 어떠하랴! 컴퓨터바둑 연구의 수준이 이 정도라면 한번 모든 걸 걸고 승부수 던지듯 벤처 기업 하나 차려보고 싶은 마음이 드는 것을.
우리말로 씌어진 컴퓨터바둑 연구
김경아, 「바둑에서 형세판단에 근거한 효율적인 정석 선택」, (경북대 컴퓨터공학과 석사 논문, 1994).
김경아, 박현수, 이종철, 「바둑에서 형세판단에 근거한 효율적인 정석 선택」, 『전자기술연구지』, 경북대 공대, Vol. 16-1, (1995), 32-40 쪽.
김영상, 「바둑 국면에서 돌의 세기와 자리의 영향력 분포에 의한 형세 평가」, 경북대학교 대학원 컴퓨터 공학과 박사학위 논문 (2000 년 12 월).
김영상, 이종철, 「컴퓨터바둑 프로그램의 설계 명세 연구」, 『전자기술연구지』, 경북대 공대, Vol. 14-1, (1993), 37-42 쪽.
김영상, 이종철, 「컴퓨터바둑 프로그래밍 기법」, 『한국정보처리학회 논문지』제 3 권 제 3 호 (96.5), 460-9 쪽.
김재형, 「컴퓨터 바둑에서 사활문제의 처리」, (연세대학교 전산과학과 석사 논문, 1994).
박현수, 「바둑에서 휴리스틱 절차를 사용한 사활문제 풀이」, (경북대 컴퓨터 공학과 석사 논문, 1994).
박현수, 임중권, 이종철, 「바둑에서 휴리스틱 함수를 사용한 사활문제 풀이에 관한 연구」, 『전자기술연구지』, 경북대 공대, Vol. 15-2, (1994), 35-43 쪽.
유정혜, 「AND/OR 신장트리를 이용한 바둑 사활 문제 풀이에 관한 연구」, (경북대 컴퓨터 공학과 석사논문, 1991).
이동기, 「초반 바둑의 계수적 형세 분석」, (경북대 공학 석사 논문, 1993).
이경자, 「후보 선정 알고리즘을 이용한 바둑 끝내기에 관한 연구」, (경북대 컴퓨터 공학과 석사 논문, 1992).
이혁순, 「가중 최대최소 역전파 알고리즘에 의한 컴퓨터바둑의 사활문제에 관한 연구」, (대전산업대학교 산업대학원 전자계산학과, 석사 논문, 1995).
임중권, 「바둑에서 후보 선택을 위한 패턴의 계층적 분류와 탐색」, (경북대 컴퓨터 공학과 석사논문, 1993).
최영숙, 「순서화된 AND/OR Pruning 을 이용한 바둑 사활의 효율 개선」, (경북대 컴퓨터 공학과 석사 논문, 1992).
'퍼온~바둑..! > 관련 자료들~' 카테고리의 다른 글
| [=] 바둑룰1 (0) | 2008.05.15 |
|---|---|
| [=] 바둑의 발견 (0) | 2008.05.13 |
| [=] 바둑의 기초이론 (0) | 2008.05.13 |
| [=] 스포츠 전문기록원에 관한 교육프로그램의 필요성 (0) | 2008.05.12 |
| [=] 레크리에이션 프로그램밍 (0) | 2008.05.12 |